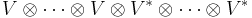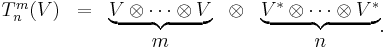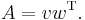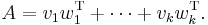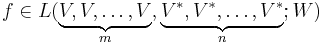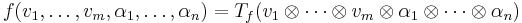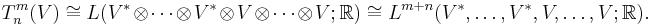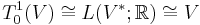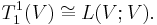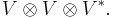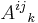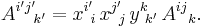Tensor (intrinsic definition)

For an introduction to the nature and significance of tensors in a broad context, see Tensor.

In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept. Their well-known properties can be derived from their definitions, as linear maps or more generally; and the rules for manipulations of tensors arise as an extension of linear algebra to multilinear algebra.

In differential geometry an intrinsic geometric statement may be described by a tensor field on a manifold, and then doesn't need to make reference to coordinates at all. The same is true in general relativity, of tensor fields describing a physical property. The component-free approach is also used heavily in abstract algebra and homological algebra, where tensors arise naturally.

Note: This article assumes an understanding of the tensor product of vector spaces without chosen bases. An overview of the subject can be found in the main tensor article.

1 Definition via tensor products of vector spaces
2 Tensor rank
3 Universal property
4 Tensor fields
5 Basis
6 References

Definition via tensor products of vector spaces

Given a finite set { V₁, ... , V_n } of vector spaces over a common field F, one may form their tensor product V₁ ⊗ ... ⊗ V_n. An element of this tensor product is referred to as a tensor (but this is not the notion of tensor discussed in this article).

A tensor on the vector space V is then defined to be an element of (i.e., a vector in) a vector space of the form:

$V \otimes \cdots \otimes V \otimes V^* \otimes \cdots \otimes V^*$

where V* is the dual space of V.

If there are m copies of V and n copies of V* in our product, the tensor is said to be of type (m, n) and contravariant of order m and covariant order n and total order m+n. The tensors of order zero are just the scalars (elements of the field F), those of contravariant order 1 are the vectors in V, and those of covariant order 1 are the one-forms in V* (for this reason the last two spaces are often called the contravariant and covariant vectors). The space of all tensors of type (m,n) is denoted

$\begin{matrix} T^m_n(V) & = & \underbrace{ V\otimes \dots \otimes V} & \otimes & \underbrace{ V^*\otimes \dots \otimes V^*} \\ & & m & & n \end{matrix}.$

The (1,1) tensors

$V \otimes V^*$

are isomorphic in a natural way to the space of linear transformations from V to V. An inner product of a real vector space V; V × V → R corresponds in a natural way to a (0,2) tensor in

$V^* \otimes V^*$

called the associated metric and usually denoted g.

Tensor rank

The term rank of a tensor is often used interchangeably with the order (or degree) of a tensor. However, it is also used in a different unrelated sense that extends the notion of the rank of a matrix given in linear algebra. The rank of a matrix is the minimum number of column vectors needed to span the range of the matrix. A matrix thus has rank one if it can be written as an outer product:

$A = v w^\mathrm{T}.\,$

More generally, the rank of a matrix is the length of the smallest decomposition of a matrix A into a sum of such outer products:

$A = v_1w_1^\mathrm{T} %2B \cdots %2B v_kw_k^\mathrm{T}.$

Similarly, a tensor of rank one (also called a simple tensor) is a tensor that can be written as a tensor product of the form

$T=a\otimes b\otimes\cdots\otimes d$

where a, b,...,d are in V or V*. That is, if the tensor is completely factorizable. In indices, a tensor of rank 1 is a tensor of the form

$T_{ij\dots}^{k\ell\dots}=a_ib_j\cdots c^kd^\ell\cdots.$

Every tensor can be expressed as a sum of rank 1 tensors. The rank of a general tensor T is defined to be the minimum number of rank 1 tensors with which it is possible to express T as a sum (Bourbaki 1988, II, §7, no. 8).

A tensor of order 1 always has rank 1 (or 0, in the case of the zero tensor). The rank of a tensor of order 2 agrees with the rank when the tensor is regarded as a matrix (Halmos 1974, §51), and can be determined from Gaussian elimination for instance. The rank of an order 3 or higher tensor is however often very hard to determine, and low rank decompositions of tensors are sometimes of great practical interest (de Groote 1987). Computational tasks such as the efficient multiplication of matrices and the efficient evaluation of polynomials can be recast as the problem of simultaneously evaluating a set of bilinear forms

$z_k = \sum_{ij} T_{ijk}x_iy_j\,$

for given inputs x_i and y_j. If a low-rank decomposition of the tensor T is known, then an efficient evaluation strategy is known (Knuth 1998, p. 506–508).

Universal property

The space 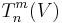$T^m_n(V)$ can be characterized by a universal property in terms of multilinear mappings. Amongst the advantages of this approach are that it gives a way to show that many linear mappings are "natural" or "geometric" (in other words are independent of any choice of basis). Explicit computational information can then be written down using bases, and this order of priorities can be more convenient than proving a formula gives rise to a natural mapping. Another aspect is that tensor products are not used only for free modules, and the "universal" approach carries over more easily to more general situations.

A scalar-valued function on a Cartesian product (or direct sum) of vector spaces

$f�: V_1\times V_2\times\cdots\times V_N \to \mathbf{R}$

is multilinear if it is linear in each argument. The space of all multlinear mappings from the product V₁×V₂×...×V_N into W is denoted L^N(V₁,V₂,...,V_N; W). When N = 1, a multilinear mapping is just an ordinary linear mapping, and the space of all linear mappings from V to W is denoted L(V;W).

The universal characterization of the tensor product implies that, for each multilinear function

$f\in L(\underbrace{V,V,\dots,V}_m,\underbrace{V^*,V^*,\dots,V^*}_n;W)$

there exists a unique linear function

$T_f \in L(V\otimes\cdots\otimes V\otimes V^*\otimes\cdots\otimes V^*; W)$

such that

$f(v_1,\dots,v_m,\alpha_1,\dots,\alpha_n) = T_f(v_1\otimes\cdots\otimes v_m\otimes\alpha_1\otimes\cdots\otimes\alpha_n)$

for all v_i ∈ V and α_i ∈ V^∗.

Using the universal property, it follows that the space of (m,n)-tensors admits a natural isomorphism

$T^m_n(V) \cong L(V^*\otimes \dots \otimes V^*\otimes V \otimes \dots \otimes V; \mathbb{R}) \cong L^{m%2Bn}(V^*,\dots,V^*,V,\dots,V;\mathbb{R}).$

In the formula above, the roles of V and V^* are reversed. In particular, one has

$T^1_0(V) \cong L(V^*;\mathbb{R}) \cong V$

and

$T^0_1(V) \cong L(V;\mathbb{R}) = V^*$

and

$T^1_1(V) \cong L(V;V).$

Tensor fields

Main article: tensor field

Differential geometry, physics and engineering must often deal with tensor fields on smooth manifolds. The term tensor is in fact sometimes used as a shorthand for tensor field. A tensor field expresses the concept of a tensor that varies from point to point.

Basis

For any given coordinate system we have a basis {e_i} for the tangent space V (this may vary from point-to-point if the manifold is not linear), and a corresponding dual basis {eⁱ} for the cotangent space V* (see dual space). The difference between the raised and lowered indices is there to remind us of the way the components transform.

For example purposes, then, take a tensor A in the space

$V \otimes V \otimes V^*.$

The components relative to our coordinate system can be written

$\mathbf{A} = A^{ij} {}_k \mathbf{e}_i \otimes \mathbf{e}_j \otimes \mathbf{e}^k$ .

Here we used the Einstein notation, a convention useful when dealing with coordinate equations: when an index variable appears both raised and lowered on the same side of an equation, we are summing over all its possible values. In physics we often use the expression

$A^{ij} {}_k\$

to represent the tensor, just as vectors are usually treated in terms of their components. This can be visualized as an n × n × n array of numbers. In a different coordinate system, say given to us as a basis {e_i'}, the components will be different. If (x^i'_i) is our transformation matrix (note it is not a tensor, since it represents a change of basis rather than a geometrical entity) and if (yⁱ_i') is its inverse, then our components vary per

$A^{i'j'}\! {}_{k'} = x^{i'}\! {}_i \, x^{j'}\! {}_j \, y^k\! {}_{k'} \, A^{ij} {}_k.$

In older texts this transformation rule often serves as the definition of a tensor. Formally, this means that tensors were introduced as specific representations of the group of all changes of coordinate systems.

References

Abraham, Ralph; Marsden, Jerrold E. (1985), Foundations of Mechanics (2 ed.), Reading, Mass.: Addison-Wesley, ISBN 0-201-40840-6 .
Bourbaki, Nicolas (1989), Elements of mathematics, Algebra I, Springer-Verlag, ISBN 3-540-64243-9 .
de Groote, H. F. (1987), Lectures on the Complexity of Bilinear Problems, Lecture Notes in Computer Science, 245, Springer, ISBN 3-540-17205-X .
Halmos, Paul (1974), Finite-dimensional Vector Spaces, Springer, ISBN 0387900934 .
Jeevanjee, Nadir (2011), An Introduction to Tensors and Group Theory for Physicists, ISBN 978-0-8176-4714-8, http://www.springer.com/new+%26+forthcoming+titles+(default)/book/978-0-8176-4714-8
Knuth, Donald (1998) [1969], The Art of Computer Programming vol. 2 (3rd ed.), pp. 145–146, ISBN 978-0-201-89684-8 .